Simultaneous equations are equations that involved two or more unknown variables. There must be as many equations as the number of unknown variables in order for us to solve the problem. There are two types of simultaneous equations, the first is linear and the second is mixed. For linear simultaneous equations, please refer to linear simultaneous equations. In this example, we will show you how to design a program that can solve mixed simultaneous equations, that is , one linear equation and one quadratic equation. The interface is as shown below:
Mixed simultaneous equations take the following form:
ax+by=m
cx2+dy2=n
Simultaneous equations can normally be solved by the substitution or elimination methods. In this program, we use the substitution method. So, we obtained the following formulas:
x1 = (m ad + Sqr(m 2 a 2 d 2 - (b 2
c + a 2 d) (d m 2 - b 2 n))) / (b 2 c + a 2 d)x2 = (m a d +-Sqr(m 2 a
2 d 2 - (b 2 c + a 2
d) (d m 2 - b 2 n))) / (b 2 c + a 2 d)
y1 = (m - a x1) / b
y2 = (m - a x2) / b
To limit the answers to two decimal places, we use the round function.The runtime interface is shown in the Figure below:
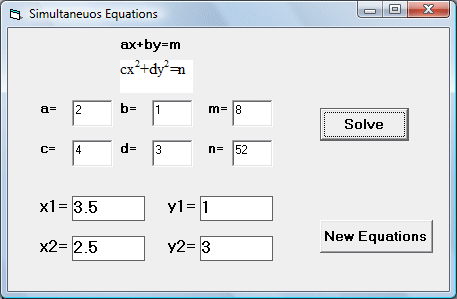
Private Sub Command1_Click()
Dim a, b, c, d, m, n As Integer
Dim x1, x2, y1, y2 As Double
a = Val(Txt_a.Text)
b = Val(Txt_b.Text)
m = Val(Txt_m.Text)
c = Val(Txt_c.Text)
d = Val(Txt_d.Text)
n = Val(Txt_n.Text)
x1 = (m * a * d + Sqr(m ^ 2 * a ^ 2 *
d ^ 2 - (b ^ 2 * c + a ^ 2 * d) * (d * m ^ 2 - b ^ 2 * n))) / (b ^ 2 * c
+ a ^ 2 * d)
x2 = (m * a * d - Sqr(m ^ 2 * a ^ 2 *
d ^ 2 - (b ^ 2 * c + a ^ 2 * d) * (d * m ^ 2 - b ^ 2 * n))) / (b ^ 2 * c
+ a ^ 2 * d)
y1 = (m - a * x1) / b
y2 = (m - a * x2) / b
Lbl_x1.Caption = Round(x1, 2)
Lbl_y1.Caption = Round(y1, 2)
Lbl_x2.Caption = Round(x2, 2)
Lbl_y2.Caption = Round(y2, 2)
End Sub
Copyright©2008 Dr.Liew Voon Kiong. All rights reserved |Contact|Privacy Policy